Ich gebe zu, dass man mit dem ggT nur das größte Quadrat findet, aber im vorliegenden Fall ist es nunmal die 5.
Man beachte, dass es sich bei den Längen schon um Angaben in mm handelt. Wie soll man da mit einer noch kleineren Teilung fertigen?
Die Aufgabe an sich, kann man durch die Primfaktorzerlegung lösen.
Nehmen wir mal an, es handelt sich um die Längen 1500mm und 2000mm. In diesem Fall sieht man sofort, dass die größten Quadrate hier die Länge 500mm haben können und 500 ist eben ggT von diesen zwei Zahlen.
Nun möchten wir aber eventuell kleinere Quadrate machen. Einige findet man sehr leicht nach kurzem Überlegen. Das wären z.B. die Kantenlängen 250mm, 100mm. Aber gibt es auch andere Möglichkeiten?
Die Primfaktorzerlegung von 1500 ist 2*2*3*5*5*5 hier ist auch die Seite hilfreich:
http://www.mathepower.com/primfaktor.php
Die Primfaktorzerlegung von 2000 ist 2*2*2*2*5*5*5
Jetzt sucht man sich die Faktoren, welche bei beiden Zahlen vorkommen, das wäre hier 2*2*5*5*5 . Die Multiplikation beliebiger Auswahl dieser Faktoren ergibt eine Zahl, durch die sowohl 1500 als auch 2000 restlos teilbar ist. Wenn man für die Auswahl alle nimmt (2*2*5*5*5) bekommt man eben die schon erwähnten 500. Man kann aber auch 5*5*5 rechnen und erhält 125. 1500mm geteilt durch 125mm ergibt 12 Teile, 2000/125 =16Teile
Man kann also 12x16 Quadrate in diesem Feld unterbringen, wobei die Kantenlänge dieser Quadrate 125mm ist.
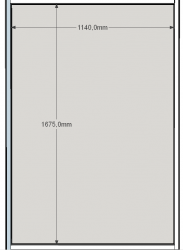
Kommen wir nun zum Feld aus dem Eröffnungsbeitrag
Bei der Primfaktorzerlegung von 1140 erhält man 2*2*3*5*19.
Angenommen, die andere Läge wäre 1596mm, die Zerlegung ergibt 2*2*3*7*19
Die gleichen Faktoren sind hier 2*2*3*19, die Multiplikation ergibt hier 228, was auch der ggT von 1140 und 1596 ist.
Das größte Quadrat für diese Kombination hat also die Länge von 228mm, kleinere sind 2*3*19=114 oder 2*2*19=76
1140/140=10 , 1596/140=14 ergibt 10*14 Quadrate mit der Kantenlänge 114mm
Jetzt haben wir uns keine Gedanken über die Sprossendicke gemacht. Es sollen 30mm sein.
Dann hätte ich den Vorschlag die eine Seite bei 1140mm zu lassen und für die andere 1608mm zu nehmen.
Damit kann man für die freien Felder (ohne die Sprossen gesehen) 204mm nehmen
Wenn die freien Felder kleiner sein sollen, dann geht es leider nur noch mit 87mm.
Ich habe es auch durchgerechnet, wenn die 1675mm unverändert bleiben sollen, aber in diesem Fall komme ich nicht nahe genug an die 1140mm.
Wer besseren Vorschlag hat, möge ihn bitte auch mitteilen. Wer einen Fehler in meinem Rechengang findet, möge das bitte aufzeigen.
Mit 0,1mm kann man das sicherlich auch rechnen, aber wie soll man das dann abmessen und sägen?
rafikus