Tauchsäge: Schiene rechtwinklig anlegen; wie macht ihr das?

[FredT]

Nur mal als Hinweil: CNC-gefräste Verleimwinkel sind auch hinreichend genau. Mit solchem Teil hätte ich den Winkelansatz der FS mal geprüft und nachgearbeitet. Ist ja kein Hexenwerk oder raketenwissenschaft. Und als Heimwerker(!) sollte man das schon mal drauf haben.
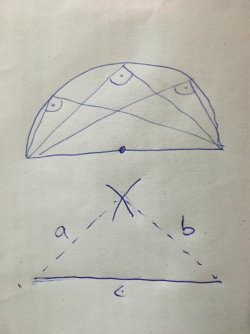
Anderwärts könnte man sich auch mal einen Referenzwinkel einer renomierten Firma mit genormter Genauigkeit zulegen. Den hat man fürs Leben. Oder eben auch einen Geowinkel checken und ggf. nacharbeiten. Richtmaß ist dabei immer der olle Phythagoras: von einer 40cm breiten Platte einen 30cm breiten Abschnitt sägen und das Eckmaß nachmessen: 50cm. Hast du mehr, mußt du die kurze Kathete nacharbeiten, hast du wenige, mußt du dort auflegen. Wie war das mit den Eulen und Athen? Genau: tragen... (Oder Mathematik Sekundarstufe)

 

[Fichtenelch]

Richtmaß ist dabei immer der olle Phythagoras: von einer 40cm breiten Platte einen 30cm breiten Abschnitt sägen und das Eckmaß nachmessen: 50cm. Hast du mehr, mußt du die kurze Kathete nacharbeiten, hast du wenige, mußt du dort auflegen. Wie war das mit den Eulen und Athen? Genau: tragen... (Oder Mathematik Sekundarstufe)

Nichts für ungut, aber ich weiß beim
besten Willen nicht warum so viele den Pythagoras nennen.
Der ist doch dafür um eine fehlende Strecke beim Dreieck zu ermitteln, richtig?
Ich hatte schon mal ein Bild angehangen was wie ich persönlich finde eine gute Hilfe für jedermann ist.

Es geht um das Verhältnis 3:4:5
Schaut einfach nochmal aufs Bild.
Pythagoras ist nicht notwendig um einen Winkel zu prüfen.

 

[dsdommi]

Na kommt doch aufs selbe raus. Wenn a und b gegeben ist kannst du dir c ausrechnen. Ist c gemessen nicht gleich c berechnet stimmt der Winkel nicht. Ist aber imho völliger Nonsens weil unnötig. Beim messen der Strecken a b c mache ich viel mehr Fehler als beim einfachen zeichnen. Aber jeder wie er denkt.

 

[Helibob]

Wie man es nennt, ist doch eigentlich fast egal (für uns nicht schwerpunkt-mäßig Mathematiker). Hauptsache man weis wie es gemeint ist und kann es sinnvoll anwenden.
Nebenbei angemerkt, es funktionieren auch andere Zahlen, die je nach benötigter Größe dann auch besser passen als nur 3:4:5 und davon ein vielfaches. Hier.
Gruß Matze

 

[Fichtenelch]

Wie man es nennt, ist doch eigentlich fast egal (für uns nicht schwerpunkt-mäßig Mathematiker). Hauptsache man weis wie es gemeint ist und kann es sinnvoll anwenden.
Nebenbei angemerkt, es funktionieren auch andere Zahlen, die je nach benötigter Größe dann auch besser passen als nur 3:4:5 und davon ein vielfaches. Hier.
Gruß Matze

Ja das ist ja die Geschichte mit dem Verhältnis.

3:4:5

Geht zum Beispiel auch für 60cm 80cm und 100cm

Anfangs wurde auf die Frage wie man es macht einfach nur mit "Pythagoras" geantwortet.
Ich persönlich könnte damit nicht viel anfangen.

 

[FredT]

Es sind ja eigentlich auch gar nicht die absoluten Zahlen, sondern das Verhältnis der Strecken zueinander. Man darf gern als Grundbasis für die Berechnung auch andere Einheiten abbilden, also zB von Parfitt das Grundmaß 32 für die Lochtische. Nur eben muß das Verhältnis 3:4:5 eingehalten sein.
Nichts anderes ist übrigens das Messen und Vergleichen der Eckmaße bei Korpen und Schubladen zur Ermittlung der Rechtwinkligkeit.

 

[Helibob]

Geht zum Beispiel auch für 60cm 80cm und 100cm

Wäre ein Beispiel für ein vielfaches der "Basis-"Zahlen 3:4:5.

das Verhältnis der Strecken zueinander

Das ist mir klar, wollte mit meine Post aber auch ergänzen, dass es nicht nur das eine Verhältnis gäbe. Wenn es auch in der Praxis das Geläufigste.
8:15:17 (oder ein vielfaches davon) würde z. B auch funktionieren.
7:24:25 ggf. wenn eine Seite im Verhältnis recht kurz?! - Wie praktikabel das jedoch dann noch ist, habe ich noch nicht ausprobiert. Könnte mir vorstellen das diese Zahlenkombi fehleranfälliger ist.
Gruß Matze

 

[Helibob]

Parfitt das Grundmaß 32

Parfitt sagt mir nix, meine Ente ist auch etwas überfordert. Kannst du das aufklären.

Ansonsten, so einen 90° Abschlag-Winkel zum Zerlegen mit der relativ günstigen Wolfcraft-Dübelschiene habe ich mir vor ein paar Jahren schon gebohrt. Wenn Interesse besteht, kann ich diesen mal fotografieren, ist gerade wieder aus der "Umzugskiste gepurzelt und fährt zusammengebaut in der noch nicht fertig Werkstatt herum".
Gruß Matze

 

[Fichtenelch]

Wäre ein Beispiel für ein vielfaches der "Basis-"Zahlen 3:4:5.

Das ist mir klar, wollte mit meine Post aber auch ergänzen, dass es nicht nur das eine Verhältnis gäbe. Wenn es auch in der Praxis das Geläufigste.
8:15:17 (oder ein vielfaches davon) würde z. B auch funktionieren.
7:24:25 ggf. wenn eine Seite im Verhältnis recht kurz?! - Wie praktikabel das jedoch dann noch ist, habe ich noch nicht ausprobiert. Könnte mir vorstellen das diese Zahlenkombi fehleranfälliger ist.
Gruß Matze

Der Gedanke ist nicht verkehrt, aber man kommt da schnell durcheinander.

Besser ist zum Beispiel,

3:4:5 gleich 6:8:10

In cm angewandt ist das auch für was kleines sehr gut.

9:12:15 12:16:20 usw...

Das ist der Weg den ich da immer wähle.


Also die Grundzahlen 3 4 5 jeweils mit dem gleichen Multiplikator.

Da kommst du an jedes Ziel, egal ob groß oder klein.
Bei so vielen Bauten schon sehr erfolgreich angewandt.

 

[woodyholgi]

Schau Dir an wie Festool das löst. Und klebe Dir einfach ein Stückchen Kunsstoff oder Alu auf den vorhandenen Anschlag, mit genau dem Überstand wie die FS hoch ist. Dann hast Du einen 2fachen Anzeiger wie z.B. Festool. Kommt dabei ja nicht auf absolute Genauigkeit an.

Guten Morgen,
gibt es das Teil von Festool als Ersatzteil?

cheers
Holger

 

[dsdommi]

Ich oute mich jetzt mal weil ich gerade auf dem Schlauch stehe.
Ich begreife einfach nicht wie ich zb bei einem Brett dass 40cmx20cm ist den rechten Winkel mit der 3 4 5 Methode prüfen kann.
Nach Pythagoras
1600+400=2000. Daraus die wurzel macht 44,721
Aber wie komme ich bei 3 4 5 auf das Maß?
Wenn ich eine Wand stellen will ist das schon klar. Da nehme ich ja das gleiche Maß für a und b zum abstecken und stecke dann c ab.
Aber mit vorgegebenen Maßen?

 

[dsdommi]

Ok ok.
Wenn ich mir auf dem Brett eine Markierung bei 15cm mache und dann die diagonale zu den 20cm messe muss die 25cm sein.
Manchmal sieht man den Wald halt nicht in dem man steht.
Ist aber doch recht Fehler behaftet finde ich.

 

[Holzfummler]

Aber wie komme ich bei 3 4 5 auf das Maß?

9 + 16 = 25

Quadrate der Maßen beachten.

 

[Fichtenelch]

Ok ok.
Wenn ich mir auf dem Brett eine Markierung bei 15cm mache und dann die diagonale zu den 20cm messe muss die 25cm sein.
Manchmal sieht man den Wald halt nicht in dem man steht.
Ist aber doch recht Fehler behaftet finde ich.

Ja genauso ist es.
Aber der Kante wo dein Winkel anliegt trägst du zum Beispiel eine Strecke von 15 cm an.
Am Ende dieser Strecke ziehst du mit deinem Winkel einen Riss, dadurch entsteht zeichnerisch eine zweite Strecke.
Auf dieser trägst du 20cm an.
Jetzt müssen zwischen beiden Enden der Strecken genau 25 cm sein, sind es zum Beispiel 25,1 ist der Winkel ungenau.
Das klappt besser als man denkt.

Wie bin ich jetzt aber auf 15 20 und 25 gekommen?

Mein Grundverhältnis ist 3:4:5

Als Multiplikator habe ich 5 gewählt, bedeutet also

3 x 5=15
4 x 5=20
5 x 5=25

9 + 16 = 25

Quadrate der Maßen beachten.

Da muss ich sagen weiß ich nicht was das bedeutet, vielleicht stehe ich auch gerade auf dem Schlauch.

Wer andere Größen haben möchte muss halt die 3 die 4 und die 5 mit einem gemeinsamen Multiplikator Erweitern.

Es ginge ja zum Beispiel auch folgendes:

3 x 1,5 = 4,5
4 x 1,5 = 6
5 x 1,5 =7,5

Wichtig ist für alle 3 Zahlen der gleiche Multiplikator, es bedarf meiner Meinung nach keine Quadrate.

 

[dsdommi]

9 + 16 = 25

Quadrate der Maßen beachten.

Die Erklärung ist mir jetzt etwas schleierhaft
Verstehe nicht was du meinst.

 

[pedder]

Ich oute mich jetzt mal weil ich gerade auf dem Schlauch stehe.
Ich begreife einfach nicht wie ich zb bei einem Brett dass 40cmx20cm ist den rechten Winkel mit der 3 4 5 Methode prüfen kann.
Nach Pythagoras
1600+400=2000. Daraus die wurzel macht 44,721
Aber wie komme ich bei 3 4 5 auf das Maß?
Wenn ich eine Wand stellen will ist das schon klar. Da nehme ich ja das gleiche Maß für a und b zum abstecken und stecke dann c ab.
Aber mit vorgegebenen Maßen?

Du willst doch einen Winkel prüfen. Der ist an allen Punkten der Katheten gleich, sofern sie denn gerade sin. Dein Brett von 40*20 misst Du dann an der 20er Kante 18cm (3*6)ab, an der 40 Kante 4*6=24cm und die Diagonale zwischen diesen Punkten muss dann genau 30cm (5*6) lang sein.

Aber ein Rechteck lässt sich noch viel leichter auf Rechtwinkligkeit überprüfen, denn beide Diagonalen müssen gleich lang sein.

 

[dsdommi]

Danke für die Erklärungen.
Hat ja dann doch noch geklappt

 

[Holzfummler]

Die Erklärung ist mir jetzt etwas schleierhaft

Hi
die Summe der Kathedenquadrate ergibt das Hypothenusenquadrat. Die Katheten bilden den rechten Winkel. Also:
(3 x 3) 9 plus (4 x 4) 16 gleich (5 x 5) 25.
Praktisch:
An der Anschlagkante die erste Kathetenlänge markieren: z. b. 30 cm
Mit Zollstock mehr oder weniger am unterem Schnittpunkt (bei den 30 cm) ansetzen und bei 40 cm einen ganz kleinen Bogen anzeichnen.
Am Null der Anschlagkante (von den 30 cm) mit Zollstock 50 cm ansetzen und wieder kleinen Bogen anzeichnen.
Da, wo sich die Bögen kreuzen ist der andere Punkt für den Schnitt.
Schau dir den vorhergehenden Screenshot an, dann fällt es dir wie Schuppen von den Augen.
LG
Thomas

 

[raziausdud]

Pythagoras : im rechtwinkligen Dreieck gilt a Quadrat + b Quadrat = c Quadrat (a hoch 2 + b hoch 2 = c hoch 2). Ich bekomm es mit dem Handy nicht besser geschrieben …

Wobei a und b die beiden am rechten Winkel anliegenden Strecken (Katheten, quasi das Dach) und c die gegenüberliegende Strecke (Hypothenuse, quasi die Basis) sind. Natürlich kann man dieses „Dach“ in allen Orientierungen (Spitze links, rechts, oben, unten) konstruieren).

Man kann alle möglichen Kombinationen wählen. Dabei ist 3:4:5 halt am besten zu merken. Und auch recht gut zu zeichnen oder zu messen, weil a und b recht groß sind.

Mit sehr kleinem a oder b (Dreieck in Form eines flachen Keils) ginge es also auch, zB mit dem Verhältnis 7:24:25 aus # 57 (ins Quadrat gesetzt wären das 49+576= 625). Nur wird das Zeichnen oder Messen dann fehleranfälliger, ähnlich wie ein Schreinerwinkel mit kurzer Anlege-Basis und langem Schenkel.

Rainer

 

[raziausdud]

Zum Konstruieren eines rechtwinkligen Dreiecks ist meines Erachtens ein ZIRKEL das beste Werkzeug.

Entweder man schlägt einen Halbkreis über c und kann da hinein beliebige rechtwinklige Dreiecke zeichnen (Skizze oben). Dazu braucht man nicht mal den Pythagoras. Und es ginge auch mit ner Schnur, nem Nagel, nem Stift und nem Lineal.

Oder man trägt die Strecken a und b nach Pythagoras mit dem Zirkel von den Endpunkten der Hypothenuse c aus ab. Wo die sich schneiden, ist der dritte Punkt des Dreiecks (Skizze unten).

 

[FleischpeitscheAusHack]

Ist die OSB-Platte denn inzwischen gesägt?

 

[dsdommi]

Und das alles um eine osb Platte parallel abzusägen. Aber danke für die Erklärungen.
Das mit dem Zirkel kommt mir irgendwie bekannt vor

 

[Helibob]

Nächster Thread: Wie bekomme ich die ganzen Zirkel- und Hilfslinien wieder spurenfrei von meiner Holzplatte!

 

[Ossei]

Ergänzend zu @raziausdud:
Nennt sich Fasskreisbogen.

 

[dsdommi]

Nächster Thread: Wie bekomme ich die ganzen Zirkel- und Hilfslinien wieder spurenfrei von meiner Holzplatte!

Radiergummi